IA8 - 機率方法在圖像去噪之應用Part 1: Binary image

在IA4的文章裡我們提到了傳輸一張binary image後，有可能會受到干擾導致圖片被污染，裡面討論了復原的方法，像是一次傳輸多張照片，最後用投票的方式來決定該像素的顏色應該取\(+1\)還是\(-1\)，因為如果噪聲是隨機的，那麼不太可能同個位置超過一半的像素都是錯的。但這個方法有個缺點，就是必須一次傳輸多張相同的圖片才能達到良好的修復效果，可是這非常地消耗數據傳輸量以及講究頻寬的大小，這對應到成本的增加，尤其是當我們要傳輸高傳真的訊號時。那麼是不是有什麼方法，可以單從一張收到的影像中去回推原始未受到污染的圖片，我想要用兩篇文章來探討，我採用由簡入繁的方式，第一篇這裡我們先處理binary image的情況，在下篇我們再進一步處理彩色的照片。

一、從圖模型檢視雜訊圖像

在IA7裡我們談到了修復刮花圖像的技術，出於圖像毀損的狀態，所以我們當初設定是刮花處與真實圖像之間並無關聯，但對於雜訊圖像則情況不同，因為這些在圖像上的雜訊，可能是原來的像素加上一個擾動值，假設真實的像素值是\(x\)，那麼加上噪聲後新的像素\(y\)就可以表示成 \[ y = x + n\tag{1} \] 其中\(n\)表示噪聲。這種加上擾動值\(n\)最常假設的生成方式便是均值為0的高斯噪聲。
　從Eq. (1)中我們假設了一個簡單的關係式。由於一整張圖片是由非常多的像素所構成一個W×H的網格，或稱陣列，其中W和H分別表示圖像寬和高所對應的像素數量，我們可以用圖模型 (graphical model, GM) 來對應真實無雜訊的圖像\(\mathbf{x}\)和觀測到存在噪聲的圖像\(\mathbf{y}\)之間的關係，見圖1，粗體字表示圖像是一個陣列而非純量。

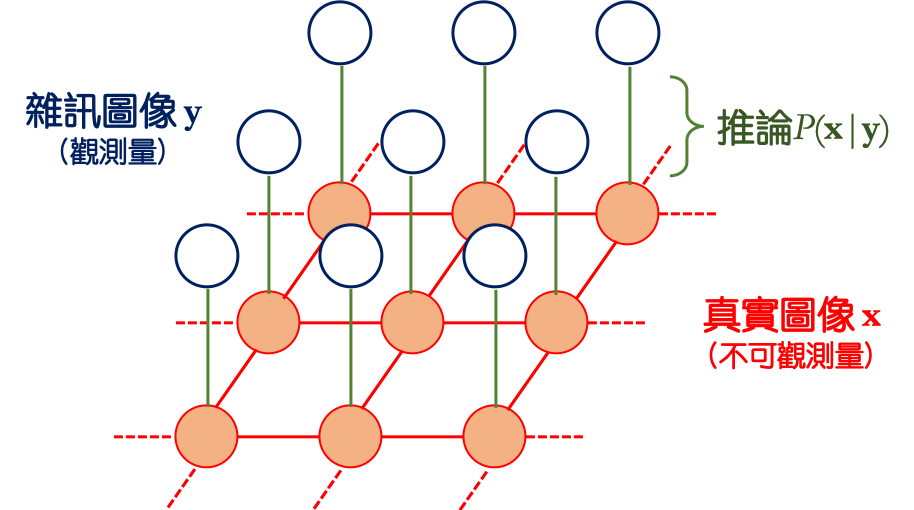圖1. 利用圖模型來推論真實圖像和雜訊圖像之間的關係

　我們認為真實圖像\(\mathbf{x}\)的每一個像素 (圖1中橘色實心的節點) 和周遭的像素都有關連，所以我們用紅色的實現將之連起，例如一張照片中一張人臉上任一處肉色的圖像一定和周圍皮膚的顏色有關聯，而不會和遙遠處天空的藍色有關聯。但我們觀測到的圖像\(\mathbf{y}\)已經被某些未知雜訊的生成機制所破壞，所以原則上這些像素點之間並不存在關聯，就如同圖1中藍色的空心節點，它們構成我們所見的圖案，彼此間沒有線將它們串連起來。而這個假定的噪聲機制便透過垂直的綠色來連接 (可以如Eq. (1)所示，或者其它的方式)，它代表的是當給定\(\mathbf{x}\)的時候，最後我們觀察到\(\mathbf{y}\)的條件機率。另外橘色節點之間的關聯其實是一個馬可夫毯 (Markov blanket)，可以見IA7的介紹。

二、清除噪聲

由於本文探討的是binary image，我們先將像素值侷限在僅有\(+1\)和\(-1\)兩種可能。所以假定一幅乾淨的圖像\(\mathbf{x}\)在某處的像素\(x_i\)，這個\(x_i\)一定和它周圍的鄰居\(\mathcal{N}\)有關聯性，當\(\mathcal{N}\)給定時，\(x_i\)最有可能是\(+1\)或\(-1\)便可以推測得出來，接著我們再給定噪聲的機制，便可以透過\(x_i\)得到\(y_i\)，而\(y_i\)即是最終被我們觀測到帶有雜訊的像素。故將上述的過程整個逆推回去，便得到了復原乾淨圖片方法的概念！
　而binary image的像素值和我們在物理雜記3所談論的Ising model本質上是一模一樣的，原則上給定\(\mathcal{N}\)後\(x_i=+1\)的機率可由Eqs. (PH3.3,PH3.4)來決定，只是它們並沒有將觀測量\(y_i\)納入考慮，所以該關係式需要修正。我們從最初的能量函數著手，並採用Bishop 2008給出的關係式 \[ E(x_i,y_i) = hx_i -\beta \sum_{j\in\mathcal{N}} x_i x_j -\eta x_i y_i, \tag{2} \] 其中\(h\)表示\(x_i\)偏好出現\(+1\)或\(-1\)的強度，當\(h=0\)代表無偏好，其實就是對應到Ising model裡的磁場強度\(H\)，因為處於外部磁場會使得自旋偏好向上或向下。而第二項則表示透過周圍環境來推論\(x_i\)的機率，其實Eq. (2)是Eq. (PH3.1)裡取\(J=1\)的特例，亦即我們認為由於圖像存在規律性，所以當周圍有較多\(+1\)時，中心像素為\(x_i=+1\)的機率會高於\(-1\)的機率。而\(\eta\)則表示觀測值\(y_i\)和真實值\(x_i\)之間連結的強度，對一個非常骯髒的圖片，我們傾向關聯小，而對較乾淨的圖片，則關聯會較大。
　因此，我們馬上可以將第一段描述逆推的過程寫成如下的機率表述 \[ P(x_i|y_i) = \frac{P(x_i,y_i)}{P(y_i)}\propto P(x_i,y_i)\tag{3} \] 而 \[ P(x_i,y_i) = \frac{e^{-E(x_i,y_i)}}{\mathcal{Z}}.\tag{4} \] 在Eq. (3)的分母\(P(y_i)\)是歸一化係數，在整個計算都是常量不用管它。所以不難從Eqs. (3,4)發現當\(x_i\)的值使能量\(E(x_i,y_i)\)最小的話，它出現的機率會最大！但接著這引入了兩種不同的概念來計算\(x_i\)的值，一種是所謂的決定性演算法 (determistic algorithm)，例如我們在IA7中使用的就屬於這類，而另一種是機率性演算法 (probabilistic algorithm)，我們將分兩小節討論。

2.1 決定性演算法

從Eqs. (3,4)中我們知道使機率出現最大等同是找能量最小，或者是 \[ \hat{x}_i ={\rm argmax}~P(x_i|y_i) = {\rm argmin}~E(x_i,y_i).\tag{5} \] 所以通過Eq. (2)，當\(y_i\)和鄰居的狀態\(\mathcal{N}\)給定的時候，不管\(x_i=+1\)或\(-1\)，我必取那個使能量最小的值\(\hat{x}_i\)，hat符號表示estimate。雖然我們一開始是從使機率最大的概念出發，但最終選取的方式卻不是隨機取樣，而是直接取一個定值，而那個定值使得機率的條件最大 (argmax)，或對應使能量最小 (argmin)。
　原則上當上述的步驟完成後得到的結果我們稱做一次迭代，但通常一次迭代後的成果不見得滿意，我們會再將該結果送進下一次迭代，不斷重複這個過程，而由於每次\(x_i\)的選擇都是使條件機率最大，所以使用決定性算法生成一系列的過程也稱作迭代條件模式 (iterated conditional modes, ICM)。ICM有個缺點就是容易陷進局域極值內而跳不出來，這與我們要找全域極值的期望相反，但優點是計算速度較快，這我們稍後再討論，接著我們來看機率性演算法。

2.2 機率性演算法

與決定性演算法不同的是，我們不直接找條件最大而是從機率的公式Eq. (4)著手，分別算出\(x_i=\pm 1\)對應的機率\(P_{\pm 1}\)，然後我們用隨機取樣的方式來決定\(x_i\)的值，即使\(+1\)出現的機率較高，通過隨機採樣，還是有可能採樣的結果給出\(\hat{x}_i=-1\)，由於這種隨機性，我們才稱作該演算法是機率性演算法。由於Eq. (4)的分佈形式稱作Gibbs分佈 (Gibbs distribution，物理學中比較常叫做Boltzmann distribution)，所以對應的採樣我們也叫它Gibbs採樣 (Gibbs sampling)。
　同2.1節所描述的，當我們掃完所有圖像陣列\(\mathbf{y}\)上的像素並完成對\(\mathbf{x}\)的採樣後我們就完成一次迭代，而通常結果必須經過多次迭代後才會比較符合我們預期的情況，當我們把這一系列迭代的結果繪成如圖2所示，那麼便構成了一條MCMC鏈。

圖2. 機率性算法得到每次迭代所構成的序列MCMC鏈

　從圖2來看，對觀測到的像素\(y_i\)而言它是永不變的，它與推論的像素之間有一條綠色的關聯，關聯強度透過Eq. (2)的\(\eta\)來調變，另外從第一次迭代完成後的結果開始 (最左)，我們先有\(x_i=+1\)，接者給定鄰居\(\mathcal{N}\)和觀測值\(y_i\)後我們可以計算\(x_i=\pm 1\)的機率\(P(\pm 1|\mathcal{N})\)，但不管則麽樣這只是機率，即使我們算出\(+1\)的機率比較大，採樣後還是有可能給出\(\hat{x}_i=-1\)的情況，如第2步所示。但這沒有關係，如果它真的應該是\(+1\)，那麼在下一步後就會自行修正。總之，Gibbs採樣這類的機率性演算法的優點是最終會逐漸穩定並收斂在全域極值處，而不會陷進局域極值的泥淖而無法自拔，但缺點是相較於ICM慢許多。

三、實作噪聲去除

那麼我們已經建立所有binary image去噪所需要的知識了，在本文隨附的源代碼裡可以參照本次所需要讀入的模組，另外操作陣列我採向量化的語言，如果對於python陣列內每個元素還習慣用for迴圈來操作的話，建議先讀一下物理雜記3，裡面有如何過渡的概念，況且binary image的情況跟Ising model如出一徹，有點概念也是好事。
　在源代碼內我建立一個產生binary image的函數binarize，原則上他接受cv2讀入的灰階圖片，並將灰階值小於閾值th的轉成\(-1\)而大於的轉成\(+1\)。對於一個binary image而言所謂的噪點便是錯誤的像素值，例如原本該要是\(+1\)的不知怎麼變成\(-1\)去了。所以噪聲可以想像成構造一個和圖像\(\mathbf{x}\)相同大小的陣列，稱作噪聲陣列\(\mathbf{n}\)，其元素不是\(1\)就是\(-1\)，當我操作矩陣乘法\(\mathbf{ nx}\)時 (不是內積)，即Eq. (1)在binary image的噪聲生成機制 \[ y_i = n_i x_i.\tag{6} \] 若\(n_i=1\)那麼\(y_i\)仍然對應到原來的\(x_i\)，亦即沒有錯誤；但若\(n_i=-1\)則\(y_i\)對應到翻號的\(x_i\)而發生錯誤，這就稱做噪聲。我們透過np.random.choice來決定\(\mathbf{n}\)有多少比例的元素是\(-1\)，而這個比例\(p\)由參數noise_rate控制，可以參考源代碼實現noisy binary image的方式 (注意若取\(p=0.5\)則代表全部打亂無法復原，當\(p>0.5\)僅僅是將黑變白白變黑，所以\(p=0.5\)可視為100%破壞了)。

圖3. 帶有噪聲的加菲貓

　讓我們生成一張噪聲比例\(p=0.3\)加菲貓binary image如圖3，現在要將它修復，不管如何我們都得計算能量函數Eq. (2)，在這裡我們恆取\(h=0\)避免困擾。唯一需要計算的就是來自\(x_i\)鄰居貢獻的求和，這可以使用correlate2d來實現 
# Input noisy binary image
im = noisy_image
# Calculate the contribution from neighbors
nei = correlate2d(im,[[1,1,1], \
                      [1,0,1], \
                      [1,1,1]],\
                      mode="same")
其中im是雜訊的圖片，nei是來自鄰居的貢獻，即每個像素\(x_i\)所對應到的\(\sum_{j\in\mathcal{N}}x_j\)的值，見Eq. (2)。接著我們便可定義能量函數了，如下 
def energy(x,y,nei,params):
    """
    Energy when x = +1 or -1
    """
    beta, eta = params[0],params[1]
    return -x*beta*nei - eta*y
其中輸入x表示\(x_i\)的值而y表示觀測值\(y_i\)，beta和eta和輸出已定義於Eq. (2)，原則上由於輸入的nei是個陣列，所以energy輸出也是個陣列，代表當我將\(\mathbf{x}\)的每個像素值都取成\(\pm 1\)時他所對應的能量。原則上就是在每個像素位置去比較到底取哪個值會讓能量最小的意思，故我可以計算 
beta, eta = 1,0.1                      # Parameters
Epos = energy(1,im,nei,[beta,eta])     # Energy if x_i = 1
Eneg = energy(-1,im,nei,[beta,eta])    # Energy if x_i = -1
所以有了能量後我就可以選擇我到底是要用ICM直接比較能量的大小來決定\(\hat{x}_i\)的值呢還是要用Gibbs採樣的方式呢？我們先講ICM，因為ICM非常簡單。

3.1 ICM實現去噪 

按Eq. (5)就是比能量大小，那個能讓能量最小的值就是我要的\(\hat{x}_i\)，毫無懸念，所以定義一個minE函數，它接受noisy imagy im，以及兩個能量Epos和Eneg分別對應到\(x_i=\pm 1\)的情況 
def minE(im,Epos,Eneg):
    """
    Smaller energy has definitive chance of appearing.
    """
    im[Epos<Eneg] = 1
    im[Eneg<Epos] = -1
    return im
所以在這裡它比了大小，對im圖像陣列而言，管它原來的值是什麼，若我發現在那個位置\(x_i=+1\)的值能使能量最小，我就強迫讓那個位置的像素變成\(+1\)，反之亦然，另外一點沒有明講的就是可能出現Epos=Eneg的情況，這種情況原則上原來im那個點的像素值是什麼就是什麼，在這次迭代中不動它，所以比完後就回傳修復的圖片。
　方便一點，直接寫一個denoise函數來實現ICM吧，如下 
def denoise(im,y,params=[1,0.3]):
    """
    Binary image denoising using ICM algorithm.
    """
    # Contributions from neighbors
    nei = correlate2d(im,[[1,1,1], \
                          [1,0,1], \
                          [1,1,1]],\
                         mode="same")
    
    # Calculate the energies of being +1 and -1 states for every pixels
    Epos = energy(1,y,nei,params)
    Eneg = energy(-1,y,nei,params)
    
    return minE(im,Epos,Eneg)
Well，原則上這不算是一個ICM，因為它只算了一次，通常要迭代數次後才能算得上是符合ICM裡那個iterated的意思😂。我們來嘗試將圖3迭代個10次看看最終的成果如何，腳本如下 
iters = 10
denoise_icm = deepcopy(noisy_image)
# 10 iterations
for i in range(iters):
    denoise_icm = denoise(denoise_icm,im)
最終結果如圖4，可以看到大部分的雜訊都被清掉了，nice!

圖4. ICM迭代10次後的結果，其中\(p=0.3\)

3.2 Gibbs採樣去噪

接下來我們就實作Gibbs採樣這種機率性演算法的去噪方式，原則上在denoise函數裡面一直到return之前都是一樣的，只是我們最後不能採行minE函數來修正。所以我要定義一個新的函數叫做gibbs，它是為了實現2.2節的內容而生。
　首先我們需要計算Eq. (4)的對\(x_i=\pm1 \)的機率，分子\(E(x_i,y_i)\)可以用3.1裡提到的energy函數來計算，所以對\(x_i=+1\)的能量就是Epos，而其機率為 
pos = np.e**(-Epos)
很簡單吧，都跟Eq. (4)長得一樣，所以對\(x_i=-1\)則是 
neg = np.e**(-Eneg)
但是我們還有一個問題，就是這些機率都是尚未歸一化的，不能直接拿來計算，為了歸一化我們需要Eq. (4)裡那個partition function \(\mathcal{Z}\)。在統計力學裡，通常會告訴你對整個系統的\(\mathcal{Z}\)不可算或很難算，這是事實，不過在圖像處理裡面我們通常一次都只看一個局部的狀態，而不是一整張圖片，所以局部下\(\mathcal{Z}\)是可解的，在這裡\(\mathcal{Z}=\)pos+neg，而出現\(x_i=+1\)歸一化後的機率就是 
p_pos = pos/(pos+neg)
當然\(x_i=-1\)就是p_neg = 1-p_pos，Vola，簡單吧！不過因為是binary系統，所以只需要知道一個機率參數另外一個就自動決定了，故我們計算的時候不需要p_neg這個東西，它的資訊已全包在p_pos裡了。其實p_pos本身也是一個陣列，而這個這列的每個元素 (一定在[0,1]之間) 就是\(x_i=+1\)的機率，我們只要follow物理雜記3裡一樣，把這個機率陣列塞進scipy.stats的函數bernoulli.rvs裡就可以得到一個採樣的陣列了，而回傳的陣列中的元素如果為1表示對應位置的像素值就是\(+1\)不用管它，但如果為0表示該處的像素值是\(-1\)，我們用代換技巧把0換成\(-1\)即可。
　所以完整的代碼實現如下 
def gibbs(Epos,Eneg):
    """
    Sampling x_i from the probability conditional on energy.
    """
    # Calculate the probabilities for being +1 at every pixels
    pos = np.e**(-Epos)
    neg = np.e**(-Eneg)
    # Probabilities of being +1 at every pixels
    p_pos = pos/(pos+neg)
    
    # Sampling a new image according to p_pos
    im = bernoulli.rvs(p=p_pos)
    # Those pixels have value 0 are actually -1
    im[im==0] = -1
    return im
這個輸出就是我們透過Gibbs採樣得到的去噪圖像，你可能會好奇我們明明就是用白努利分佈為什麼要叫Gibbs採樣？因為這個系統只有雙值，就像投硬幣只會出現正反兩面一樣，所以每一次採樣都是一個白努利試驗 (Bernoulli trial)，但由於出現正面 (這裡表\(x_i=+1\)) 的機率是由Gibbs分佈給定 (Eq. (4))，所以我們還是稱這個過程叫Gibbs採樣而不是什麼白努利採樣，這裡的白努利分佈生成的隨機變數rvs只是我們用來實現從Gibbs分佈中採樣的一種手段而已，但它不用來決定誰出現的機率。最後我們寫下完整的denoise函數
def denoise(im,y,params=[1,0.3]):
    """
    Binary image denoising using Gibbs sampling.
    """
    # Contributions from neighbors
    nei = correlate2d(im,[[1,1,1], \
                          [1,0,1], \
                          [1,1,1]],\
                         mode="same")
    
    # Calculate the energies of being +1 and -1 states for every pixels
    Epos = energy(1,y,nei,params)
    Eneg = energy(-1,y,nei,params)
    
    return gibbs(Epos,Eneg)
一樣對圖3迭代10次後的去噪圖如圖5所示。

圖5. Gibbs採樣迭代10次後的結果，其中\(p=0.3\)

　如果仔細比較圖5和圖4的話，會發現Gibbs採樣的去噪結果相較於ICM來得更優秀，相同迭代次數下得到更乾淨的圖片，圖4上黑色噪點的數量顯然用肉眼就看得出比圖5來得多，這就是在第2節內所提到的ICM容易陷在局域極值而不是全域極值的最佳解上，但Gibbs採樣這種MCMC的方法反而可以避開這個缺陷，作為代價的是計算時間。
　但其實我們真的比較一下，同樣的計算方式ICM耗時0.9秒而Gibbs耗時3.2秒，這個差距不到\(\mathcal{O}(10)\)，但卻可以得到更乾淨的圖像，我認為Gibbs採樣是更優秀的選擇，我們將會在第4節討論這件事，特別是當雜訊率\(p\)非常高的時候！附註我們的加菲貓圖片是一張1595×1024超過166萬個像素的圖片，10次迭代需要處理近乎2000萬次的計算，這個時間的耗費是可以接受的！如果採用for迴圈保證等到天荒地老😅

3.3 ICM與Gibbs採樣的偽代碼

這裡我們給出兩種去噪演算法的偽代碼，方便不同語言間的轉換，兩種演算法的起頭都是一樣的，首先初始化：
  1. 計算圖片上某個像素位置\(x_i\)周圍鄰居的貢獻\({\tt nei}=\sum_{j\in \mathcal{N}}x_j\)
    (\(\mathcal{N}\)的大小可自訂，本文採計8個相鄰的像素)
  2. 利用Eq. (2)和\(\tt nei\)計算在圖像\(x_i\)處若\(x_i=\pm 1\)分別對應的能量\(E_\pm\)
  3. 選擇ICM (呼叫minE函數) 或Gibbs採樣 (呼叫gibbs函數) 去噪
若選擇ICM，minE函數：
  1. 在\(x_i\)處比較\(E_\pm\)的大小，若：
    \(E_+<E_-\)則取\(x_i=+1\)反之取\(x_i=-1\)
  2. 重複直到圖片上所有的像素\(x_i\)都被掃過一次並賦予可使局部能量最小的值為止
  3. 完成一次迭代，回傳新圖像
  4. (選用) 使用上一步回傳的新圖像並重複1.~6.的步驟直到迭代過程滿足停止條件
若選擇Gibbs採樣，gibbs函數：
  1. 在\(x_i\)處通過\(E_\pm\)和Eq. (4)計算\(x_i=\pm 1\)的機率\(P_{\pm 1}\)
    (記得要歸一化，請參照前面python腳本中gibbs函數的做法)
  2. 將\(P_{+1}\)作為輸入參數並做一次白努利試驗，若試驗結果：
    出現\(1\)，取\(x_i=+1\)
    出現\(0\)，取\(x_i=-1\)
    (該試驗也可以改用一個古老的Metropolis-Hatings演算法取代，這裡不贅述)
  3. 重複直到圖片上所有的像素\(x_i\)都被掃過一次並賦予採樣後的結果為止
  4. 完成一次迭代，回傳新圖像
  5. (選用) 使用上一步回傳的新圖像並重複1.~7.的步驟直到迭代過程滿足停止條件
以上就是本文中去噪演算法的偽代碼，原則上我是以逐元素 (element-wise) 的方式描述，就是用for迴圈來一次處理一個影像陣列的元素，這也許表較貼近C/C++和FORTRAN等語言的做法，但如同前文所述，在python裡應該使用向量化的方式以獲得更有效率的執行速度。

四、比較：ICM與Gibbs採樣去噪

從前文看來Gibbs採樣在相同迭代次數下似乎有比ICM來的乾淨，但或許可以說我如果將ICM在迭代多次一點也可以得到和Gibbs採樣一樣好的結果，況且說不定耗費的時間還比Gibbs採樣來得快。但真的是這樣的嗎？讓我們來測試一下，但為了凸顯結果，我們提高噪聲率到\(p=0.35\)，結果如圖6和圖7。

圖6. ICM去噪，經過不同迭代次數後的結果
圖7. Gibbs採樣法去噪，經過不同迭代次數後的結果

　不難發現對ICM算法而言，經過10次迭代和20次迭代的結果幾乎沒有差別，而且仍然存在著肉眼可辨識的噪點，幾乎可以確定的是，ICM去噪最優的結果大約在第7次之後就不再增加了，殘留的噪聲並無法通過更多次的迭代而去除，整個結果被truncated在某個特定的解下，而這個解並不是最優解，最優解應該是要盡力消除掉噪聲，即使它需要通過更多次的迭代！
　但Gibbs採樣這種機率性算法則展示了完全不同的結果，不僅僅在相同的迭代次數底下它能達成比ICM更好的去噪效果，而且Gibbs採樣法並不會被truncated在某個特定的解下，隨著迭代次數的增加，它的結果不斷的優化，噪聲不停的減少，整體來說朝著全域最優解前進。
　原則上決定性算法是以局域狀態當中，找出一條覺得是最好的路來前進，但局域最好的也許不能通到全域最優的狀態，它容易最後卡在某個窪地而發現沒有足夠的能量來跳出這個窪地，又由於我的步伐都是決定性的，既然我已經不夠能量了，那我就卡在這吧。但機率性算法則反其道而行，由於每一步都是由機率選定，即使今天我走的步驟讓我卡在某個窪地，但因為下一步我要往哪走也還是機率的問題，就算我發現我的能量不夠，但從前面在做採樣的過程，即使小機率也有機會出現，所以我還是有機會穿隧出這個窪地困境，並朝向全域最佳，即最低的地方邁進，這便是隨機性的力量！

五、小結

在這篇文章裡我討論了兩種去噪方式，一種是決定性一種是隨機性，而從結果來看，隨機性在達成更優解的競賽中表現較決定性的方式來的更好。本文中去噪的範例，特別是能量函數，可以視為是一個正規化函數 (regularization function)，也有些文獻或書籍稱作損失函數 (loss function)，常見的有\(L_2\) (自高斯分佈導出，對所有觀測點都折衷，sensitive to outliers) 和\(L_1\) (自Laplace分佈導出，robust to outliers) norms，以及揉和兩者優點的Huber loss function，而最佳化 (optimization) 的方案則是要最小化損失，所以Eq. (5)所謂的 \[ \hat{x}={\rm argmin}~E(x,y) \] 本質上就是為了找出那個\(\hat{x}\)成全minimize loss function這件事，而能量公式內的那些和周圍鄰居的關係則是條件限制 (constraints)。
　像ICM這種決定性演算法雖然一開始是從機率的想法出發，要找出一個參數使得它發生的機率最大 (這裡是\(\hat{x}\)在哪個值的時候最有可能出現)，但為了增進計算效率，所以透過將它改寫成數學上等價的找使能量最小的參數，而這個轉譯的過程也導致了從隨機性的問題變成確定性的問題，只有導致損失最小的那個參數才會被挑出來，其它都不在乎了。但由於我們也只能考慮每個像素的鄰居，亦即對每個像素在每次迭代的修正，它都只能按照局域 (local) 的訊息來最佳化，這種確定性或稱決定性的過程，很容易顧此失彼，雖然我在這步局域上看起來是最優，但不能保證現在這樣取一定會走向全局最優 (globally optimized)，最終的結果容易被truncated在某個局域的窪地裡。但由於ICM是短視的，只注重周遭而已，每個像素發現：「啊，很好啊，我都在能量最低處了，所以我沒有跳出這個地方的必要！」況且決定性算法也不可能允許我再去選擇一個新的但是會讓能量增加的態，因為這與argmin E(x,y)的相抵觸，可是我們會發現全局看起來根本不是最優，從圖6來看，第10次和第20次迭代的結果是一樣的，殘餘的噪點還是去不掉，整個解的過程其實在第7-8步就已經陷入死胡同了！
　而隨機性算法則反其道而行，它回歸最初的本質，也就是一開始的機率這一步，我不改寫成等價的argmin E(x,y)，因為既然每個態\(x\)機率可以算，其實我就已經找出了機率分佈，我唯一要做的就是從這個分佈中採樣出可能的解，這也是我們在建立Gibbs演算時必須分別求出\(P_{\pm 1}\)，再透過這個權重去隨機選擇\(x=\pm 1\)的情況。這裡會發生和決定性算法違背的情況便是即使小機率的態也有可能會被採樣出來，it's just a matter of chance，對隨機性而言這沒什麼大不了的，但對決定性演算法ICM而言這完全不可能發生的！但這個讓小機率發生的狀況卻能使我們避開陷進僅僅是局域最佳而無法自拔的窘境。假使現在Gibbs採樣的結果進入了像ICM的第7或8步那樣所有的局域都已經進入最佳的狀態 (但不是全局最優，因為還有一堆噪點)，在隨機採樣的過程中，會有幾個像素也許會跳到新的態，就算僅僅只有幾個，這幾個微小的擾動卻發展出漣漪效應在接下來的迭代中不斷擴散出去 (就像蝴蝶效應一樣，或是宇宙的結構也來自原初的重力擾動，否則宇宙現在應該是均勻了無生氣的狀態)，所以整個全局不會被鎖死在局域最優的解上，這種隨機性幫助我們能跨過中途的障礙邁並ascending到更優越的地方！
　另外從演化的過程來看，我們一直都以為著像人類如此精巧的生物，背後一定有什麼高等的智慧在操縱著我們的進化，但事實上，從這個簡單的binary image denoise的pet project來看，由於我們每個人都處在local的狀態，從local得到的資訊也有限，所以對local來說最好的途徑或許根本不會引領我們進化到更高的層次，所以大自然、或說宇宙、生命的出現，都是從一堆隨機性的現象當中所發跡，沒有什麼難解的智慧，唯有從雜亂中出淤泥而不染，透過隨機性的選擇，或許才能讓人類今日走到現在高度，或許還能用下個百年或千年的時間邁向下一個進化的巔峰！


Source on github: IA8_binary_denoise.ipynb

留言

張貼留言

這個網誌中的熱門文章

物理雜記3 - Ising模型與模擬退火

圖片
Ising模型主要是用來描述物質的鐵磁性 (ferromagnetism)，是由德國物理學家Ernst Ising在1920左右提出了處理一維的解析解。該模型包含了每個晶格上原子的自旋 (spin) 參數，兩兩相鄰的原子彼此間可以是偏好處在共同的態上 (都是自旋向上)  或是處在相反的態上 (一上一下)，而外部的磁場會對該晶格上的自旋狀態施加能量，導致其偏向某一個方向。在這篇文章裡，我們不重複Ising當年複雜的數學解析解，而且該解也只能適用在1D的狀態，對於2D以上的系統目前並沒有解析解，所以我們將要另闢蹊徑，採用MCMC模擬的方式來決定一個系統終態每個晶格上自旋的排列情形。 一、Ising模型簡介 考慮一個由圖1所構成的晶格系統，晶格上的點都代表一顆原子，而黑白則表原子的自旋狀態，我們用黑表示向下而白表示向上，所以這個binary系統可以用更簡潔的\(\pm 1\)來表示每個原子可能的自旋 (即這個系統的樣本空間\(\Omega=\{+1,-1\}\))，另外為了方便，我們採用物理學的習慣將自旋表示為希臘字母\(\sigma_{n}\)，下標\(n\)可以想像成在 n 處原子的自旋態。原則上討論的都是一個由費米子 (fermions) 構成的系統，所以自旋應該用\(\pm \frac{1}{2}\)來表述，但在計算機上我們用\(\pm 1\)比較乾脆且簡潔。另外補充一下冷知識自然界已知的物質幾乎由費米子構成，僅有媒介作用力的粒子是玻色子 (bosons)，它們的差別在於費米子有半整數 (即不能約化成整數的分數) 自旋而玻色子則是整數自旋。 圖1. 晶格系統，黑白點分別代表該處原子的自旋狀態，黑表向下，白表向上。紅色的箭頭指出中心原子的4位鄰居\(m\) 　Ising模型假定了每個晶格上的原子的自旋都會受其鄰居 (neighbors \(\mathcal{N}\)) 的狀態影響，例如圖1中間白色的原子雖然他在這一刻是處在\(+1\)的狀態，但根據其週邊四個鄰居 (分別是3白1黑) 的況，它仍有一定的機會會在下一刻翻轉自旋的狀態。 　對一個給定位置 n 的原子，它和它的周圍鄰居構成的局部區域 (local area) 形成的一個系統的能量由Ising模型給出 \[ E_n = -\sum_{m\in \mathcal{N}} J
閱讀完整內容

PS7 - 小專題: 為何高斯分佈擁有最大熵?

圖片
高爾頓板，或稱做quincunx，是由Galton爵士 (1822-1911) 所發明用來驗證中央極限定理 (CLT) 的裝置。它也是第一位討論均值回歸 (regression to the mean) 現象的科學家，但同時亦是優生學 (eugenics) 這樣錯誤觀念的推廣者 在 上篇雜記 的結尾我們提到了對於一個趨於穩態的系統擁有最大的熵，而這也是統計力學的直接應用，用物理的角度來講便是當系統平衡時 Gibbs 自由能不再變化 (\(\Delta G =0\))，而在此時會對應到系統的熵有全域極大值 (global maximum)。故大自然很多現象都已經處於穩態的狀況下，我們對這個現象的母體做抽樣，所得到的觀測樣本應也有最大熵，則描述這些觀測樣本最好的分佈便是符合該條件下擁有最大熵的機率分佈。而指數族的分佈符合最大熵的特點，我們在這個小專題內便嘗試證明高斯與二項式分佈在連續和離散的隨機變量下的條件擁有最大熵的性質。 一、機率熵 在 上篇雜記 裡裡我們探討了夏儂熵，或者稱作資訊量\(I\)的意含，所以一個系統內 (我們這裡就不再用系綜這種彆扭的歷史名詞了) 每個成員出現的機率是\(p_i\)，則對該系統的熵可以用夏儂熵公式來表示 \[ I(p) = -\sum_i p_i \ln p_i. \tag{7.1} \] 所以對某一組 連續 機率分佈函數\(p(x)\)，其中\(x\)是隨機變量，則將(7.1)的求和符號改成積分後有 \[ I(p) = -\int p(x)\ln p(x) dx, \tag{7.2} \] 稱為機率分佈\(p(x)\)的 機率熵 ，而積分的上下限則看隨機變量的範圍，例如高斯分佈就是\(\pm \infty\)。如果今天我們有兩組機率分佈\(p(x)\)和\(q(x)\)，我們便可以定義它們之間的 相對熵 ，或稱作 KL散度 (Kullback-Leibler divergence)，定義為 \[ D_{KL}(q,p)\equiv\int q(x)\ln \left(\frac{q(x)}{p(x)}\right) dx = I(q,p)-I(q)\geq 0, \tag{7.3} \] 是 正定的 (positively defined)，其中 \[ I(q,p)=-\int q(x)\ln p(x) d
閱讀完整內容

IA9a - K-means分群與EM算法: 理論

圖片
市場內分門別類的產品 原則上 K-means分群 是 EM算法 (expectation-maximization algorithm) 的一個特例，相較於EM從似然函數 (likelihood) 的方式出發並導出不同資料點對不同群 (或稱聚類、簇，cluster) 的貢獻度，K-means單純用歐氏距離來分類，雖然這加快了K-means算法的計算效率，但顯然的這麼naïve的方法會產生明顯的缺陷。但仍讓我們會先從簡單的K-means開始，並探討K-means算法的結果在某些情況下和人類肉眼辨識的結論會產生明顯的歧義，接著再推進到通用的EM算法，除了 python 的demo外，我也會證明在數學上如何從EM得到K-means的極限 (僅限高斯混合的情況)，而在這個part內，讓我們先從數學理論的角度來面。 一、K-means分群 今天如果我有一大坨資料共120個點如圖1所示，從資料的散佈趨勢來看，很明顯的分成兩群，那我們是不是可以有一個演算法來自動化將資料點如同我們臆測的一樣分成兩袋？一個最簡單的發法便是使用K-means分群，而這個大寫K表示群的數量，以圖1而言，我們猜測K=2，所以是個2-means分群問題。 圖1. 資料散佈圖 (普魯士藍) 與初始化的紅綠兩點 　所以為了達成分群，我們需要先初始化兩個點，這兩個點代表兩群的中心。事實上，初始化的位置不必要一定剛好在兩群的中心，可以是任意挑選的地方，但為了計算方便，我們會將起始化的兩點開始在靠近資料點的平均值附近，如同圖1中紅綠兩點。我們將這兩個初始化的點叫作\(p_k\)其中\(k=1,2\)表示第\(k\)群。另外將資料點的集合用\(\mathbf{D}=\{d_1,d_2\cdots d_n \cdots d_{120}\}\)表示，所以我們計算每個點\(d_n=(x_{d_n},y_{d_n})\)和\(p_k=(x_{p_k},y_{p_k})\)的歐氏距離 \[ \ell_{n,k}=\sqrt{(x_{d_n}-x_{p_k})^2+(y_{d_n}-y_{p_k})^2}. \tag{1} \] 若該點和\(p_1\)的距離小於和\(p_2\)的距離 (\(\ell_{n,1}<\ell_{n,2}\))，則我們說\(d_n\)比較靠近\(p_1\)且應該
閱讀完整內容